参考:https://blog.csdn.net/liuxiao214/article/details/81037416
归一化层,目前主要有这几个方法,Batch Normalization(2015年)、Layer Normalization(2016年)、Instance Normalization(2017年)、Group Normalization(2018年)、Switchable Normalization(2019年);
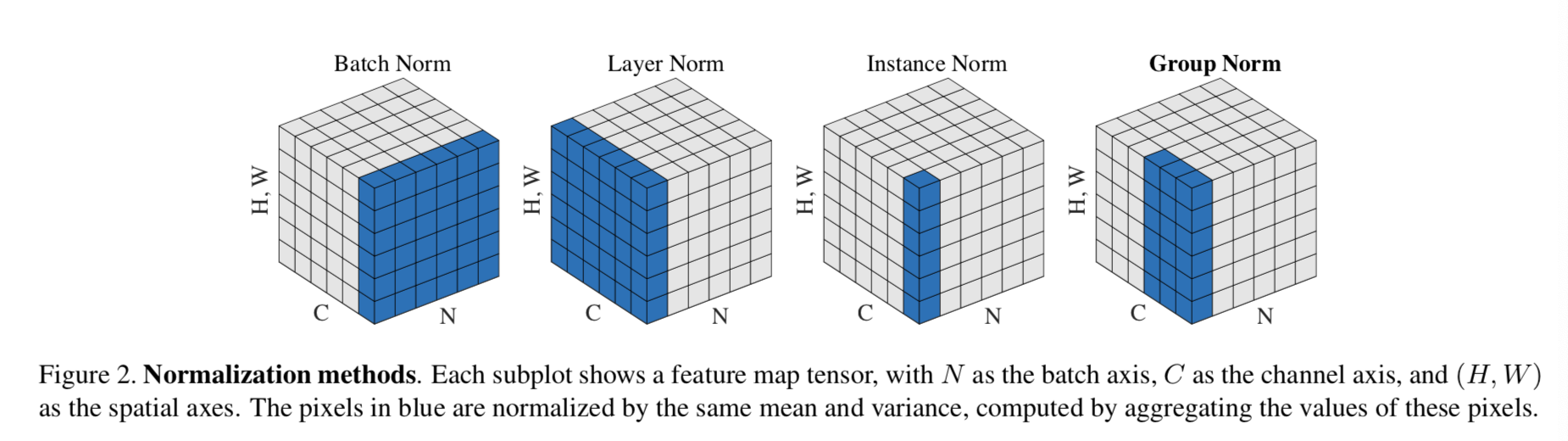
将输入的图像shape记为[N, C, H, W],这几个方法主要的区别就是在,- batchNorm是在batch上,对NHW做归一化,对小batchsize效果不好;
- layerNorm在通道方向上,对CHW归一化,主要对RNN作用明显;
- instanceNorm在图像像素上,对HW做归一化,用在风格化迁移;
- GroupNorm将channel分组,然后再做归一化;
- SwitchableNorm是将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
1.BN
batchNorm是在batch上,对NHW做归一化;即是将同一个batch中的所有样本的同一层特征图抽出来一起求mean和variance
加快收敛速度,允许网络使用更高的学习率。可作为一个正则化器,减少对dropout的需求
但是当batch size较小时(小于16时),效果会变差,这时使用group norm可能得到的效果会更好
class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)
对小批量(mini-batch)3d数据组成的4d输入进行批标准化(Batch Normalization)操作
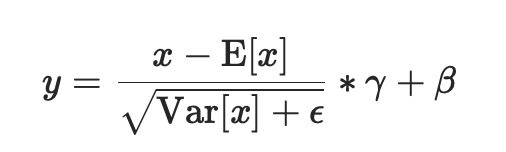
进行了两步操作:可见
- 先对输入进行归一化,E(x)为计算的均值,Var(x)为计算的方差
- 然后对归一化的结果进行缩放和平移,设置affine=True,即意味着weight(γ)和bias(β)将被使用
在每一个小批量(mini-batch)数据中,计算输入各个维度的均值和标准差。γ与β是可学习的大小为C的参数向量(C为输入大小)。默认γ取值为U(0,1),β设置为0
同样,默认情况下,在训练期间,该层将运行其计算的平均值和方差的估计值,然后在验证期间使用这些估计值(即训练求得的均值/方差)进行标准化。运行估计(running statistics)时保持默认momentum为0.1。
如果track_running_stats被设置为False,那么这个层就不会继续运行验证,并且在验证期间也会使用批处理统计信息。
⚠️这个momentum参数不同于优化器optimizer类中使用的momentum参数和momentum的传统概念。从数学上讲,这里运行统计数据的更新规则是 :
- x是估计的数据
- xt是新的观察到的数据
xnew = (1-momentum) * x + momentum * xt
因为批处理规范化是在C维(channel通道维度)上完成的,计算(N,H,W)片上的统计信息,所以通常将其称为空间批处理规范化。
参数:
- num_features: C来自期待的输入大小(N,C,H,W)
- eps: 即上面式子中分母的ε ,为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- momentum: 动态均值和动态方差所使用的动量。默认为0.1。
- affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数,即γ与β。
- track_running_stats:一个布尔值,当设置为True时,该模块跟踪运行的平均值和方差,当设置为False时,该模块不跟踪此类统计数据,并且始终在train和eval模式中使用批处理统计数据。默认值:True
Shape:
输入:(N, C,H, W)
输出:(N, C, H, W)(输入输出相同)
举例:
当affine=True时
import torchfrom torch import nnm = nn.BatchNorm2d(2,affine=True)print(m.weight)print(m.bias)input = torch.randn(1,2,3,4) print(input) output = m(input) print(output) print(output.size())
返回:
Parameter containing:tensor([0.5247, 0.4397], requires_grad=True)Parameter containing:tensor([0., 0.], requires_grad=True) tensor([[[[ 0.8316, -1.6250, 0.9072, 0.2746], [ 0.4579, -0.2228, 0.4685, 1.2020], [ 0.8648, -1.2116, 1.0224, 0.7295]], [[ 0.4387, -0.8889, -0.8999, -0.2775], [ 2.4837, -0.4111, -0.6032, -2.3912], [ 0.5622, -0.0770, -0.0107, -0.6245]]]]) tensor([[[[ 0.3205, -1.1840, 0.3668, -0.0206], [ 0.0916, -0.3252, 0.0982, 0.5474], [ 0.3409, -0.9308, 0.4373, 0.2580]], [[ 0.2664, -0.2666, -0.2710, -0.0211], [ 1.0874, -0.0747, -0.1518, -0.8697], [ 0.3160, 0.0594, 0.0860, -0.1604]]]], grad_fn=) torch.Size([1, 2, 3, 4])
当affine=False时
import torchfrom torch import nnm = nn.BatchNorm2d(2,affine=False)print(m.weight)print(m.bias)input = torch.randn(1,2,3,4) print(input) output = m(input) print(output) print(output.size())
返回:
NoneNonetensor([[[[-1.5365, 0.2642, 1.0482, 2.0938], [-0.0906, 1.8446, 0.7762, 1.2987], [-2.4138, -0.5368, -1.2173, 0.2574]], [[ 0.2518, -1.9633, -0.0487, -0.0317], [-0.9511, 0.2488, 0.3887, 1.4182], [-0.1422, 0.4096, 1.4740, 0.5241]]]]) tensor([[[[-1.2739, 0.0870, 0.6795, 1.4698], [-0.1811, 1.2814, 0.4740, 0.8689], [-1.9368, -0.5183, -1.0326, 0.0819]], [[ 0.1353, -2.3571, -0.2028, -0.1837], [-1.2182, 0.1320, 0.2894, 1.4478], [-0.3080, 0.3129, 1.5106, 0.4417]]]]) torch.Size([1, 2, 3, 4])
2.InstanceNorm2d(当mini-batch时使用)
instanceNorm在图像像素上,对HW做归一化;即是对batch中的单个样本的每一层特征图抽出来一层层求mean和variance,与batch size无关。若特征层为1,即C=1,准则instance norm的值为输入本身
CLASS torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
在4D输入上应用instance Normalization(带有额外channel维度的mini-batch 2D输入),即shape为[N,C,H,W]
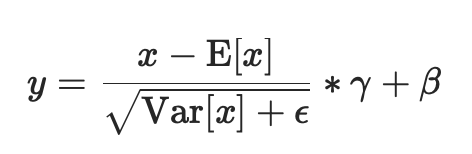
在mini-batch中的对象的均值和标准差是每个维度分开计算的。如果affine=True,则γ和β这两个可学习的参数向量,大小为C,C为输入大小。
这一层使用从训练和评估模式的输入数据计算得到的instace数据。
如果track_running_stats被设置为True,那么在训练期间,该层将继续运行计算均值和方差的估计,得到的均值和方差将使用到评估(eval)时的normalization中。运行估计时保持默认momentum为0.1。
⚠️这个momentum参数不同于优化器optimizer类中使用的momentum参数和momentum的传统概念。从数学上讲,这里运行统计数据的更新规则是 :
- x是估计的数据
- xt是新的观察到的数据
xnew = (1-momentum) * x + momentum * xt
⚠️
InstanceNorm2d和LayerNorm非常相似,但是有一些细微的差别。InstanceNorm2d应用于RGB图像等信道数据的每个信道,而LayerNorm通常应用于整个样本,并且通常用于NLP任务。此外,LayerNorm应用元素仿射变换,而InstanceNorm2d通常不应用仿射变换。
参数:
- num_features: C来自期待的输入大小(N,C,H,W)
- eps: 即上面式子中分母的ε ,为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- momentum: 动态均值和动态方差所使用的动量。默认为0.1。
- affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数,即γ与β。
- track_running_stats:一个布尔值,当设置为True时,该模块跟踪运行的平均值和方差,当设置为False时,该模块不跟踪此类统计数据,并且始终在train和eval模式中使用批处理统计数据。默认值:False
Shape:
输入:(N, C,H, W)
输出:(N, C, H, W)(输入输出相同)
举例:
import torchinput = torch.randn(2,3,2,2)input
返回:


tensor([[[[-0.9262, 0.1619], [ 2.3522, 1.2739]], [[-2.1725, 1.3967], [ 1.4407, 1.3133]], [[-0.8386, -1.1728], [-3.0443, -0.3651]]], [[[ 0.9468, -0.9257], [ 0.5376, 0.4858]], [[ 1.1766, 0.4704], [ 0.8294, -0.3892]], [[ 0.2836, 0.5864], [-0.3070, 0.3229]]]])
import torch.nn as nn#声明仿射变换要写成#m = nn.InstanceNorm2d(3, affine=True)m = nn.InstanceNorm2d(3)#feature数量,即channel number = 3output = m(input)output
返回:


tensor([[[[-1.3413, -0.4523], [ 1.3373, 0.4563]], [[-1.7313, 0.5856], [ 0.6141, 0.5315]], [[ 0.5082, 0.1794], [-1.6616, 0.9740]]], [[[ 0.9683, -1.6761], [ 0.3904, 0.3173]], [[ 1.1246, -0.0883], [ 0.5283, -1.5646]], [[ 0.1903, 1.1173], [-1.6182, 0.3106]]]])
3.LayerNorm(当mini-batch时使用)
layerNorm在通道方向上,对CHW归一化;即是将batch中的单个样本的每一层特征图抽出来一起求一个mean和variance,与batch size无关,不同通道有着相同的均值和方差
CLASS torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
平均值和标准偏差分别计算在最后几个维数上,这些维数必须是normalized_shape指定的形状。如果elementwise_affine=True,则γ和β为两个可学习的仿射变换参数向量,大小为normalized_shape
⚠️与batch normalization和instance normalization不同,batch normalization使用affine选项为每个通道/平面应用标量尺度γ和偏差β,而layer normalization使用elementwise_affine参数为每个元素应用尺度和偏差。
这一层使用从训练和评估模式的输入数据计算得到的统计数据。
参数:
- normalized_shape ( or or torch.Size): 来自期待输入大小的输入形状

如果使用单个整数,则将其视为一个单例列表,并且此模块将在最后一个维度上进行规范化,而最后一个维度应该具有特定的大小。
- eps: 即上面式子中分母的ε ,为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- elementwise_affine: 一个布尔值,当设置为True时,此模块具有可学习的元素仿射参数,γ初始化为1(表示权重)和β初始化为0(表示偏差)。默认值:True。
Shape:
输入:(N, *)
输出:(N, *)(输入输出相同)
举例:
import torchinput = torch.randn(2,3,2,2)input
返回:


tensor([[[[-0.9262, 0.1619], [ 2.3522, 1.2739]], [[-2.1725, 1.3967], [ 1.4407, 1.3133]], [[-0.8386, -1.1728], [-3.0443, -0.3651]]], [[[ 0.9468, -0.9257], [ 0.5376, 0.4858]], [[ 1.1766, 0.4704], [ 0.8294, -0.3892]], [[ 0.2836, 0.5864], [-0.3070, 0.3229]]]])
import torch.nn as nn#取消仿射变换要写成#m = nn.LayerNorm(input.size()[1:], elementwise_affine=False)m1 = nn.LayerNorm(input.size()[1:])#input.size()[1:]为torch.Size([3, 2, 2])output1 = m1(input)output1
返回:


tensor([[[[-0.5555, 0.1331], [ 1.5192, 0.8368]], [[-1.3442, 0.9146], [ 0.9423, 0.8618]], [[-0.5001, -0.7116], [-1.8959, -0.2004]]], [[[ 1.0599, -2.1829], [ 0.3512, 0.2616]], [[ 1.4578, 0.2348], [ 0.8565, -1.2537]], [[-0.0887, 0.4357], [-1.1115, -0.0206]]]], grad_fn=)
#只normalize后两个维度m2 = nn.LayerNorm([2,2])output2 = m2(input)output2
返回:


tensor([[[[-1.3413, -0.4523], [ 1.3373, 0.4563]], [[-1.7313, 0.5856], [ 0.6141, 0.5315]], [[ 0.5082, 0.1794], [-1.6616, 0.9740]]], [[[ 0.9683, -1.6761], [ 0.3904, 0.3173]], [[ 1.1246, -0.0883], [ 0.5283, -1.5646]], [[ 0.1903, 1.1173], [-1.6182, 0.3106]]]], grad_fn=)
#只normalize最后一个维度m3 = nn.LayerNorm(2)output3 = m3(input)output3
返回:


tensor([[[[-1.0000, 1.0000], [ 1.0000, -1.0000]], [[-1.0000, 1.0000], [ 0.9988, -0.9988]], [[ 0.9998, -0.9998], [-1.0000, 1.0000]]], [[[ 1.0000, -1.0000], [ 0.9926, -0.9926]], [[ 1.0000, -1.0000], [ 1.0000, -1.0000]], [[-0.9998, 0.9998], [-0.9999, 0.9999]]]], grad_fn=)
4.GroupNorm(当mini-batch时使用)
GroupNorm将channel分组;即是将batch中的单个样本的G层特征图抽出来一起求mean和variance,与batch size无关
当batch size较小时(小于16时),使用该normalization方法效果更好
CLASS torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)
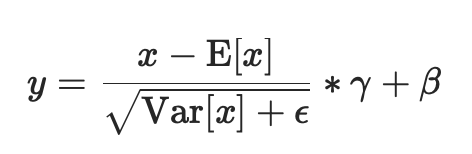
输入通道被分成num_groups组,每个组包含num_channels / num_groups个通道。每组的均值和标准差分开计算。如果affine=True,则γ和β这两个可学习的通道仿射变换参数向量的大小为num_channels。
这一层使用从训练和评估模式的输入数据计算得到的统计数据。
参数:
- num_features(int): 将通道分成的组的数量
- num_channels(int):输入期待的通道数
- eps: 即上面式子中分母的ε ,为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数,即γ与β。
Shape:
输入:(N, C,*) ,C = num_channels
输出:(N, C, *)(输入输出相同)
举例:
import torchinput = torch.randn(2,4,3,3)input
返回:


tensor([[[[-0.9154, 0.7312, 1.0657], [ 0.1783, 1.4014, 1.3043], [-0.7661, -0.6346, 0.7620]], [[ 0.9533, 2.1763, 0.4636], [ 0.0624, -0.0880, 1.2591], [ 0.5080, 0.2156, 0.0312]], [[ 0.2077, -0.2373, 0.2203], [-0.0628, -0.4680, -0.0094], [ 0.8615, 0.8549, 0.4138]], [[ 1.2188, -0.6487, 1.9315], [-1.0211, -0.1721, 0.6426], [-0.8192, 1.1049, 0.3663]]], [[[ 1.7522, -0.5378, -0.6105], [ 0.0658, -0.5731, 0.8737], [-0.2006, 0.3185, 0.6959]], [[ 0.5581, -1.5815, 0.3467], [-1.7975, 1.1900, -0.0935], [-0.7640, -0.7520, -1.2672]], [[-0.3703, 1.8731, -0.4689], [ 0.3615, 1.7101, 0.7305], [-0.0244, -0.5019, 0.3259]], [[-0.1413, -0.7416, -0.0747], [-0.6557, 0.5025, -0.0574], [ 0.2727, 2.2837, 1.6237]]]])
import torch.nn as nn#将4个通道分为2组m1 = nn.GroupNorm(2,4)output1 = m1(input)output1
返回:


tensor([[[[-1.7640, 0.3119, 0.7336], [-0.3852, 1.1568, 1.0344], [-1.5757, -1.4099, 0.3508]], [[ 0.5919, 2.1338, -0.0254], [-0.5312, -0.7208, 0.9774], [ 0.0305, -0.3381, -0.5706]], [[-0.0478, -0.6420, -0.0310], [-0.4090, -0.9500, -0.3377], [ 0.8251, 0.8163, 0.2273]], [[ 1.3022, -1.1914, 2.2539], [-1.6886, -0.5550, 0.5328], [-1.4190, 1.1501, 0.1639]]], [[[ 2.0315, -0.4375, -0.5158], [ 0.2133, -0.4755, 1.0844], [-0.0739, 0.4858, 0.8927]], [[ 0.7441, -1.5628, 0.5162], [-1.7956, 1.4254, 0.0415], [-0.6814, -0.6685, -1.2239]], [[-0.8227, 1.6729, -0.9325], [-0.0087, 1.4915, 0.4018], [-0.4380, -0.9692, -0.0482]], [[-0.5680, -1.2358, -0.4939], [-1.1402, 0.1482, -0.4747], [-0.1075, 2.1296, 1.3954]]]], grad_fn=)
#将4个通道分为4组,等价于Instance Normm2 = nn.GroupNorm(4,4)output2 = m2(input)output2
返回:


tensor([[[[-1.4648, 0.4451, 0.8332], [-0.1962, 1.2226, 1.1099], [-1.2916, -1.1390, 0.4809]], [[ 0.4819, 2.2510, -0.2265], [-0.8068, -1.0243, 0.9242], [-0.1623, -0.5852, -0.8520]], [[ 0.0230, -1.0124, 0.0523], [-0.6064, -1.5490, -0.4821], [ 1.5439, 1.5284, 0.5023]], [[ 0.9624, -0.9711, 1.7004], [-1.3567, -0.4777, 0.3659], [-1.1476, 0.8445, 0.0798]]], [[[ 2.0642, -0.9777, -1.0742], [-0.1760, -1.0246, 0.8973], [-0.5298, 0.1598, 0.6611]], [[ 1.0550, -1.1571, 0.8364], [-1.3803, 1.7083, 0.3813], [-0.3119, -0.2995, -0.8321]], [[-0.9221, 1.7498, -1.0396], [-0.0506, 1.5556, 0.3889], [-0.5102, -1.0789, -0.0929]], [[-0.4993, -1.1290, -0.4294], [-1.0388, 0.1761, -0.4113], [-0.0650, 2.0445, 1.3521]]]], grad_fn=)
#将4个通道分为4组,等价于layer Normm3 = nn.GroupNorm(4,4)output3 = m3(input)output3
返回:


tensor([[[[-1.4648, 0.4451, 0.8332], [-0.1962, 1.2226, 1.1099], [-1.2916, -1.1390, 0.4809]], [[ 0.4819, 2.2510, -0.2265], [-0.8068, -1.0243, 0.9242], [-0.1623, -0.5852, -0.8520]], [[ 0.0230, -1.0124, 0.0523], [-0.6064, -1.5490, -0.4821], [ 1.5439, 1.5284, 0.5023]], [[ 0.9624, -0.9711, 1.7004], [-1.3567, -0.4777, 0.3659], [-1.1476, 0.8445, 0.0798]]], [[[ 2.0642, -0.9777, -1.0742], [-0.1760, -1.0246, 0.8973], [-0.5298, 0.1598, 0.6611]], [[ 1.0550, -1.1571, 0.8364], [-1.3803, 1.7083, 0.3813], [-0.3119, -0.2995, -0.8321]], [[-0.9221, 1.7498, -1.0396], [-0.0506, 1.5556, 0.3889], [-0.5102, -1.0789, -0.0929]], [[-0.4993, -1.1290, -0.4294], [-1.0388, 0.1761, -0.4113], [-0.0650, 2.0445, 1.3521]]]], grad_fn=)
pix2pix代码中该部分的使用:
class Identity(nn.Module): def forward(self, x): return xdef get_norm_layer(norm_type='instance'): """返回标准化层 Parameters: norm_type (str) -- 标准化层的名字,有: batch | instance | none 对于BatchNorm,我们使用可学习的仿射参数并追踪运行数据(mean/stddev) 对于InstanceNorm,我们不使用可学习的仿射参数也不追踪运行数据 """ if norm_type == 'batch': norm_layer = functools.partial(nn.BatchNorm2d, affine=True, track_running_stats=True) elif norm_type == 'instance': norm_layer = functools.partial(nn.InstanceNorm2d, affine=False, track_running_stats=False) elif norm_type == 'none': norm_layer = lambda x: Identity() else: raise NotImplementedError('normalization layer [%s] is not found' % norm_type) return norm_layer